Mesures astrométriques accessibles à l’astro-amateur – Partie 1

Bien que l’astronomie pratiquée par l’amateur se base à l’origine sur l’observation visuelle ‒ utilisant donc des instruments optiques, et non des instruments de mesure de grandeurs physiques ‒ il peut être intéressant de procéder à des mesures simples qui ne requièrent pas d’instrumentation particulière. En effet, les distances et les dimensions en jeu sont tellement disproportionnées comparativement à ce que nous connaissons à notre échelle, que se doter de références, se donner des ordres de grandeur peut aider à s’y retrouver. Ainsi, considérer que le diamètre apparent de la lune ‒ ainsi que celui du soleil ‒représente environ 30 minutes d’arc permet d’apprécier certaines autres distances en se référant à cette mesure : La lune devient en quelque sorte un mètre étalon, et constitue ainsi notre premier instrument de mesure !

Il peut donc être utile d’utiliser des références afin de pouvoir apprécier, par exemple, la séparation de deux objets, la taille angulaire d’un autre, ou encore d’estimer la dimension d’un détail visible sur la surface de la lune. Pour ce faire, il est question d’utiliser un oculaire réticulé. Un réticule seul ne permet pas de mesurer quoi que ce soit, cependant : Selon la longueur focale de l’instrument et de l’oculaire dans lequel il est monté, ses graduations ne donneront pas la même mesure. Il est donc nécessaire d’effectuer quelques calculs avant de pouvoir l’exploiter :

Pour connaître la distance angulaire entre deux graduations (sd) séparées par exemple de 1mm dans le plan focal :

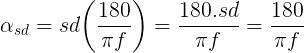
Avec :

• α : distance angulaire en arcseconde ;
• ƒ : focale de l’instrument ;
• sd : Scale Division, distance entre deux graduations, par exemple sur le réticule ci-dessous, doté de 60 graduations sur une échelle de 6mm, les graduation font 0,1mm, donc sd vaudrait pour ce réticule 100µm.

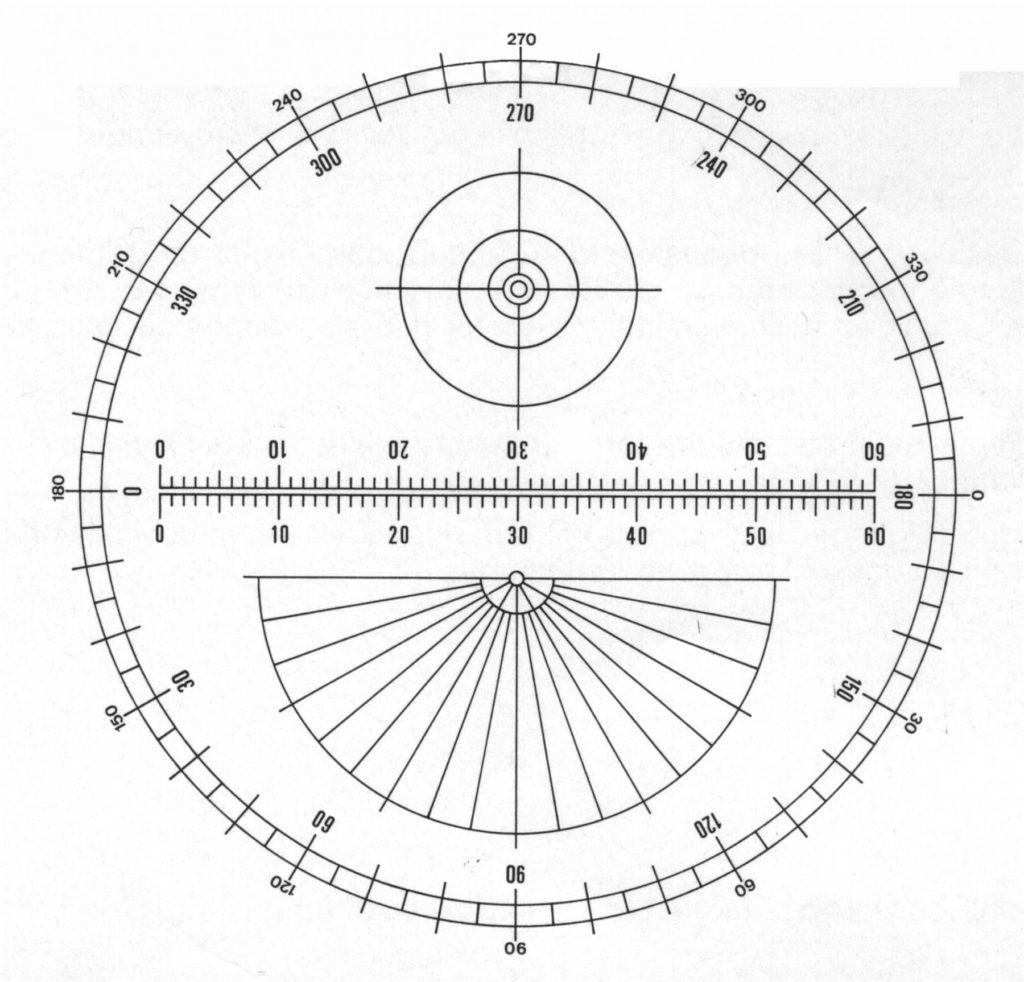
Si en revanche l’échelle est différente sur votre réticule, comme sur l’exemple ci-dessous, qui indique 0,5mm par division :

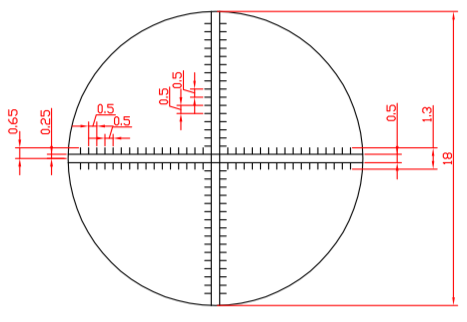
La distance angulaire devient alors dans ce cas :

Pour rappel, un radian vaut environ 57,3° ou 57° 18′ (360°÷2π) (c’est de là que provient le 180°÷π de notre équation)

L’angle en arcseconde correspondant à une graduation peut aussi se déterminer par une méthode dite du Star Drift : il est question de laisser une étoile de déclinaison δ dériver sur l’axe gradué (que l’on aura pris soin d’orienter de telle sorte que la trajectoire apparente de l’étoile soit confondue avec celui-ci). En chronométrant le temps t que met l’étoile pour franchir L graduations, il est possible de calculer l’angle α_d correspondant à une graduation :

Cette méthode reposant tout de même sur un chronométrage manuel, elle donne des résultats imprécis : Il est donc conseillé de faire plusieurs mesures et d’en calculer la moyenne afin d’approcher au mieux la valeur exacte. À titre indicatif la dérive due à la rotation de la Terre représente 15° par heure (360°/24h), soit 15 arcminutes par minute, soit encore 15 arcsecondes par seconde.

Travaux pratiques !

Méthode du Star Drift

Afin d’obtenir la meilleure précision possible pour le star drift, la déclinaison δ de l’étoile choisie sera le plus proche possible de 0°, pour obtenir un cos(δ) le plus proche de 1 possible. Notre réticule comporte 33 graduations sur chacun des 2 axes. Il est question dans un premier temps d’aligner d’un de ces axes avec la trajectoire apparente en ascension droite de l’étoile. Pour notre exemple, nous choisissons δ Orionis (Mintaka) dans la ceinture d’Orion, dont la déclinaison est -00°17′18.56″.

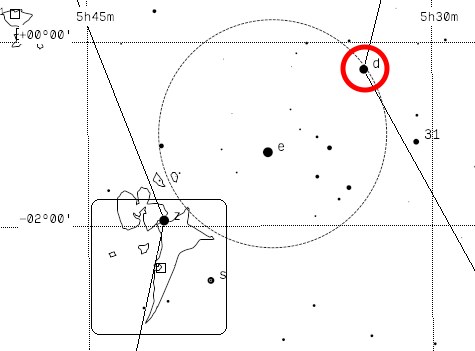
Nous la positionnons sur l’une des extrémités de l’axe que nous avons aligné avec l’équateur. À l’aide de la commande d’ascension droite, on s’assure qu’elle suive l’axe, et corrigeons l’orientation du réticule si nécessaire, jusqu’à ce que sa trajectoire se confonde avec l’axe gradué. Dans les conditions de notre observation, elle devra se placer sur la graduation la plus à droite, et nous la laisserons dériver jusqu’à la dernière graduation située à gauche. Pour cela, nous stoppons le suivi stellaire, re-positionnons précisément l’étoile sur la graduation, et démarrons le chronomètre. À compter de cet instant, l’étoile glisse lentement sur l’axe, jusqu’à ce que la dernière graduation soit atteinte, à cet instant nous stopperons le chronomètre.

Sur un télescope Newton 150/750 doté d’un oculaire Baader Polaris I 25mm, elle mettra 5′04″ soit 304 secondes pour parcourir l’ensemble des graduations. Cela nous donne :

Une graduation de cet oculaire sur un télescope de 750mm de focale donne donc 2,3 minutes d’arc (0,038°).

Notez que pour faire les choses bien, et comme indiqué précédemment, il eut fallu faire plusieurs mesures et calculer la moyenne des résultats obtenus.

Vérification

Vérifions notre calcul, en tentant de mesurer la séparation angulaire θ entre deux étoiles proches (elles n’ont pas besoin d’être dans le même système). Alcor (81,7 AL) et Mizar (85,8 AL), dans la Grande Ourse (séparées selon Cartes du Ciel de 11′48,5″) me semblent de très bonnes candidates pour cet exercice !

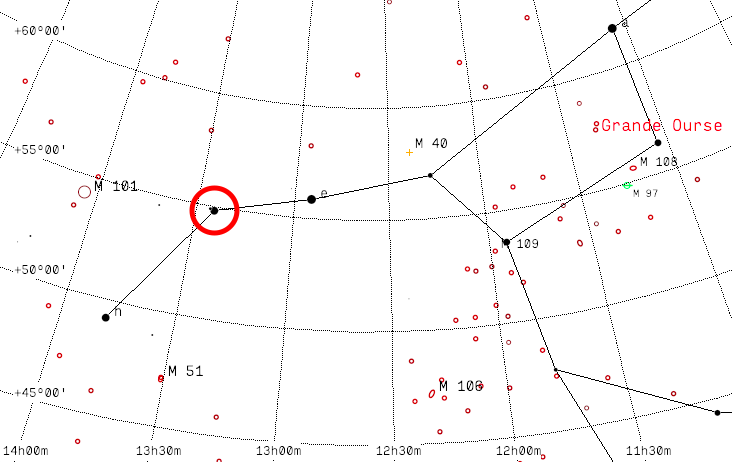
En regardant de plus près la zone cerclée de rouge, l’astre apparemment unique laisse place à deux objets distincts :

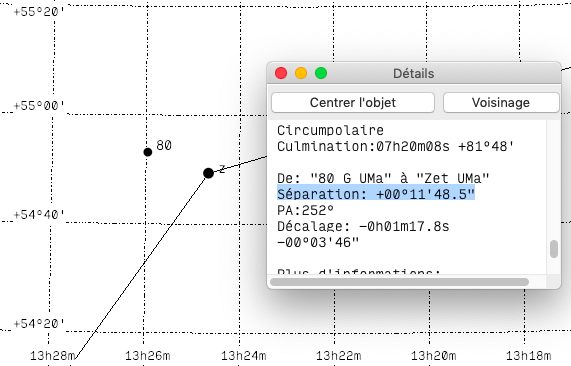
Après avoir pointé l’instrument sur ζ Ursa Majoris alias «Mizar», la plus lumineuse de ces deux étoiles, il est question de pointer l’instrument pour obtenir les deux étoiles dans le champ, et d’orienter l’oculaire pour qu’elles soient toutes deux sur l’un des axes gradués. Il suffit alors de positionner Mizar sur une graduation et de compter le nombre de graduation la séparant de Alcor :

Notre relevé effectué sur le terrain (et par grand froid !) nous donne environ 5,2 graduations. Puisque chaque graduation vaut 2,309′, calculons la séparation θ :

Bingo 🙂 Si nous retenons notre valeur arrondie de 2,3′, nous obtenons 11,96′ de séparation, ce qui est tout à fait acceptable et comparable à la séparation de 12′ annoncée par SkySafari, ou à celle annoncée par Carte du Ciel 00°11′48,5″ (11,576′) notamment au regard des imprécisions de la lecture (absence de sous divisions notamment).

Par ailleurs, si nous souhaitons calculer notre longueur focale réelle, c’est possible en ré-injectant nos résultats dans la première équation :

(Attention, ici l’oculaire présente des graduations espacées de 0,5mm, nous multiplions notre valeur d’angle par deux, ou nous utilisons 90° plutôt que 180°, cela revient au même)

Nous obtenons donc environ 754mm pour un instrument qui était annoncé à 750mm… cela confirme que notre calcul est sinon exact, au moins cohérent et assez proche de la réalité.

Conclusion de cette première partie

Nous avons pu étalonner notre oculaire réticulé avec une assez bonne précision, via deux méthodes qui sont assez simple à mettre en œuvre. Il resterait éventuellement à refaire cet étalonnage pour le cas où une lentille de barlow est utilisée, afin de pouvoir procéder à des mesures plus fines.

C’est précisément ce que ferons dans la deuxième partie, et cela nous permettra d’estimer les dimensions de détails sur la lune.